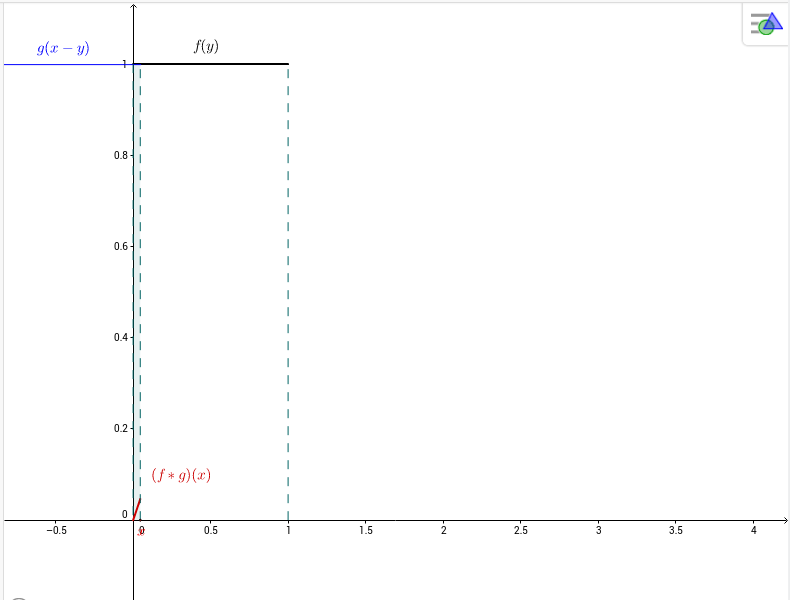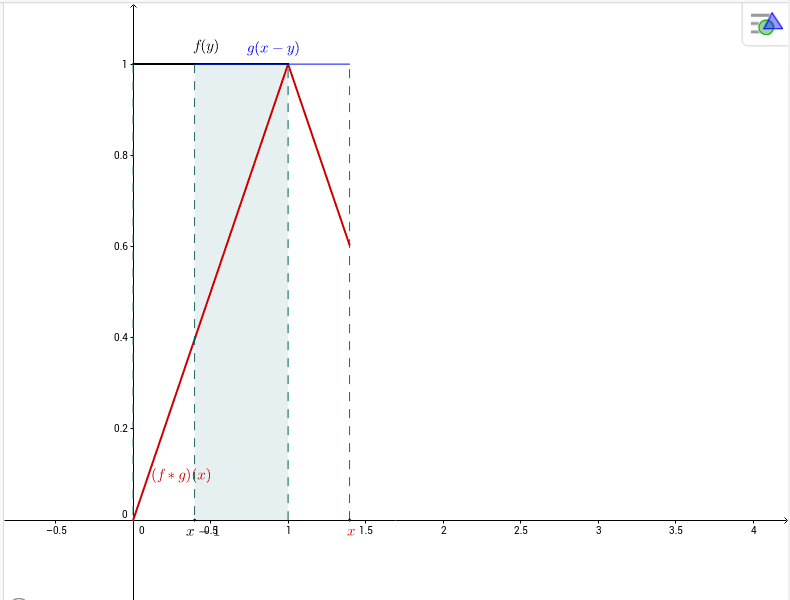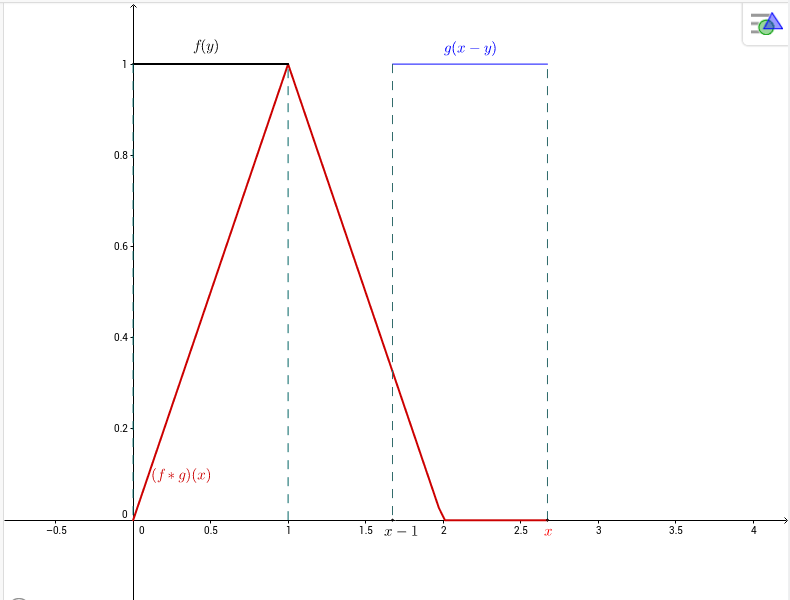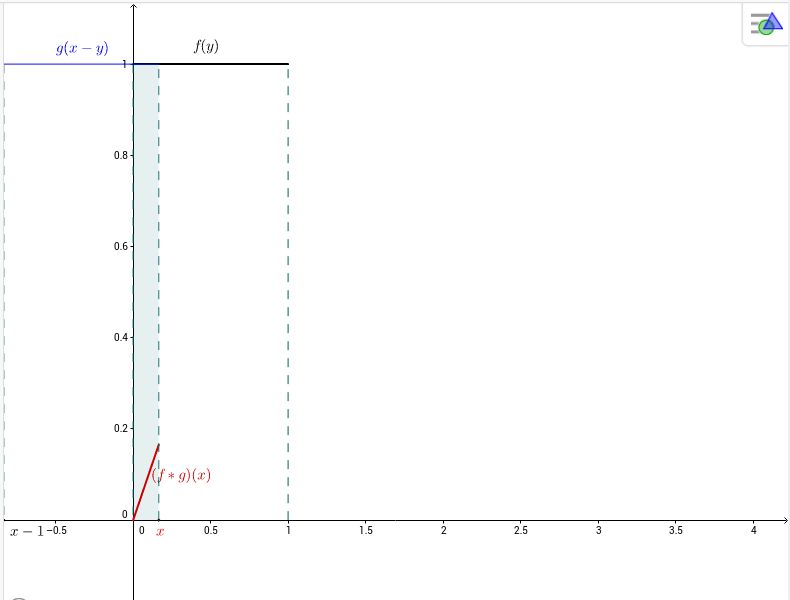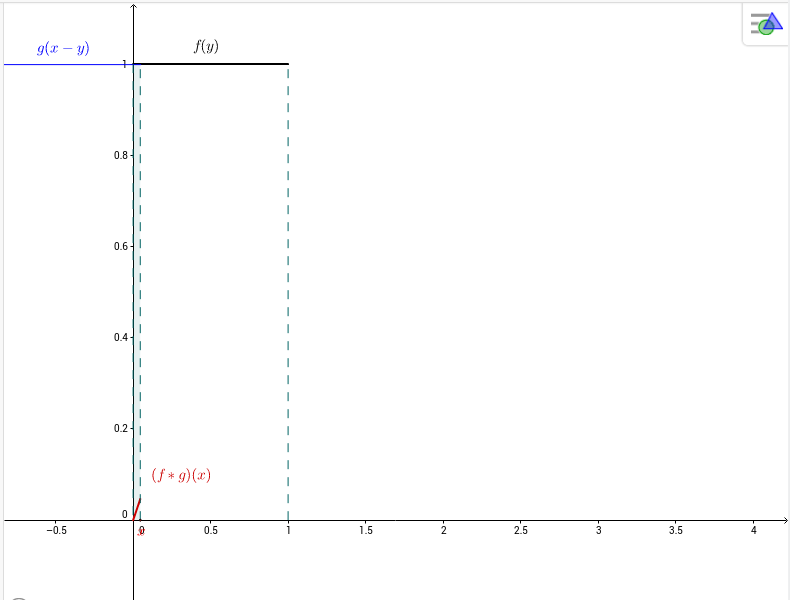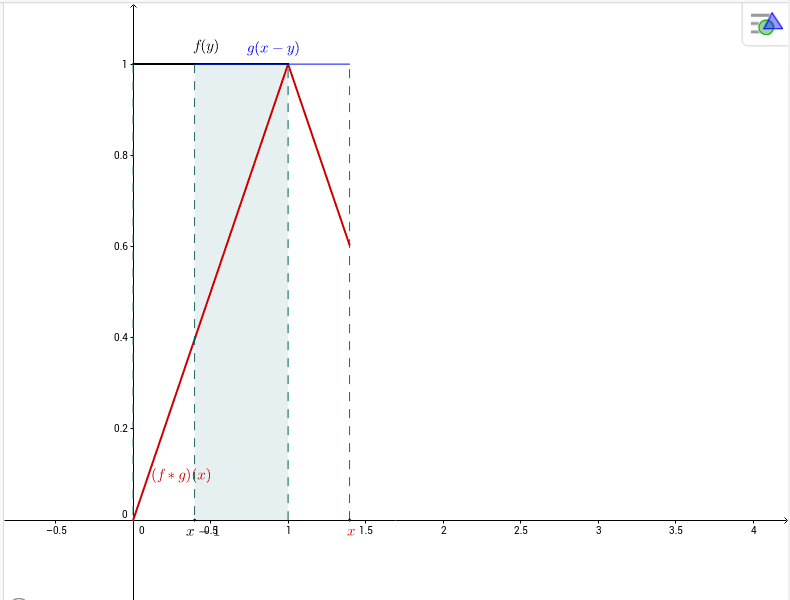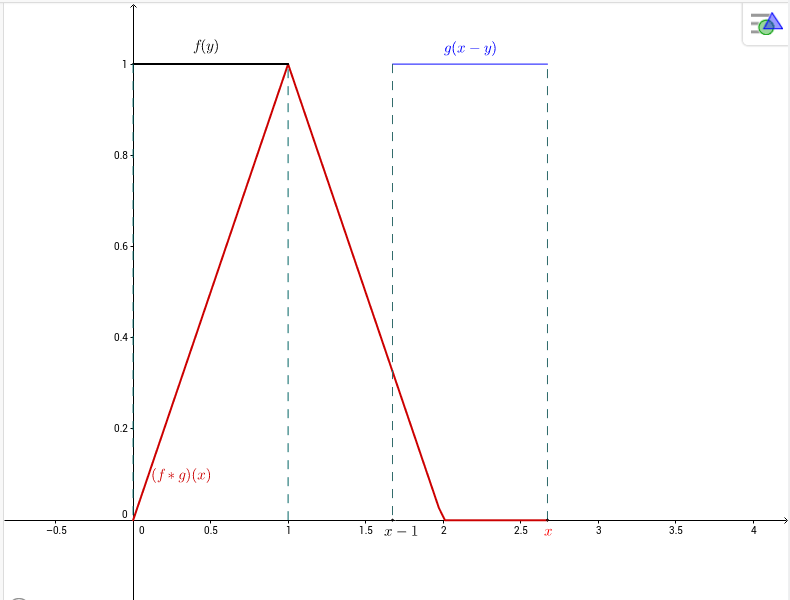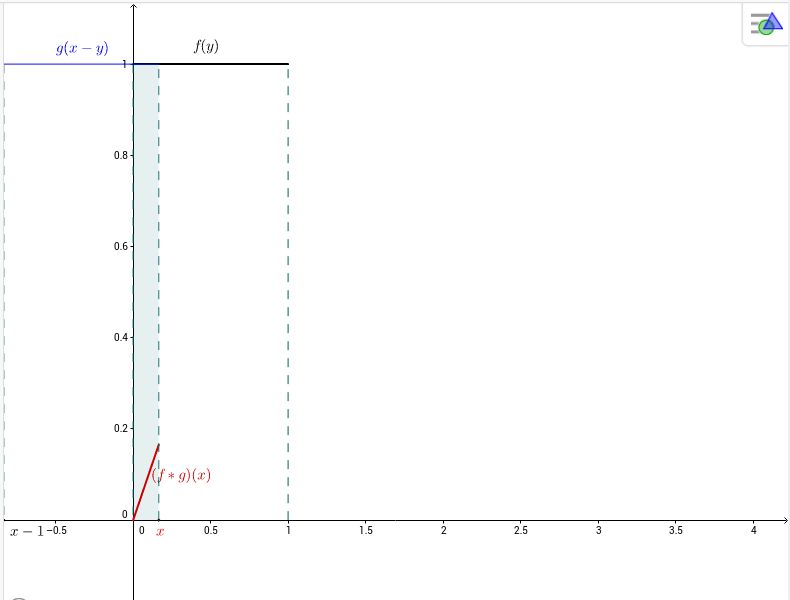Animações de Convolução
- A convolução de duas
funções $f,g:[0,\infty)\rightarrow\mathbb{R}$ é uma função
definida por
$$(f*g)(t)=\int_0^tf(t-\tau)g(\tau)d\tau,\quad \mbox{para }t\ge 0. $$
Considere
$$f(t)=g(t)=\begin{cases}1,&\text{ se } 0< t< 1,\\0,&\text{caso contrário}
\end{cases}$$
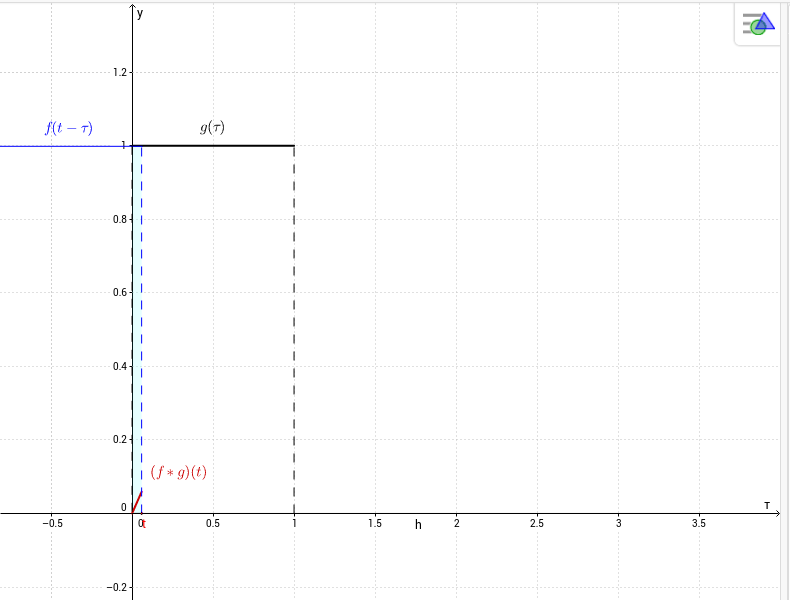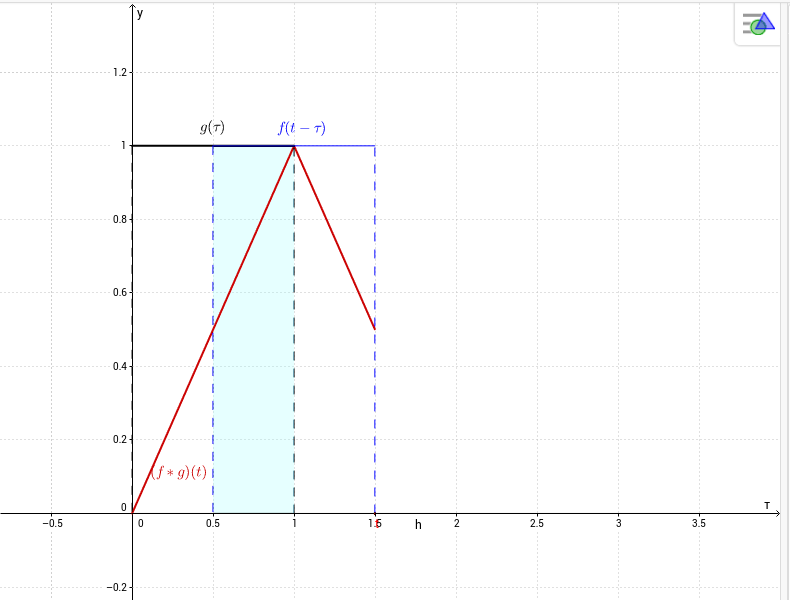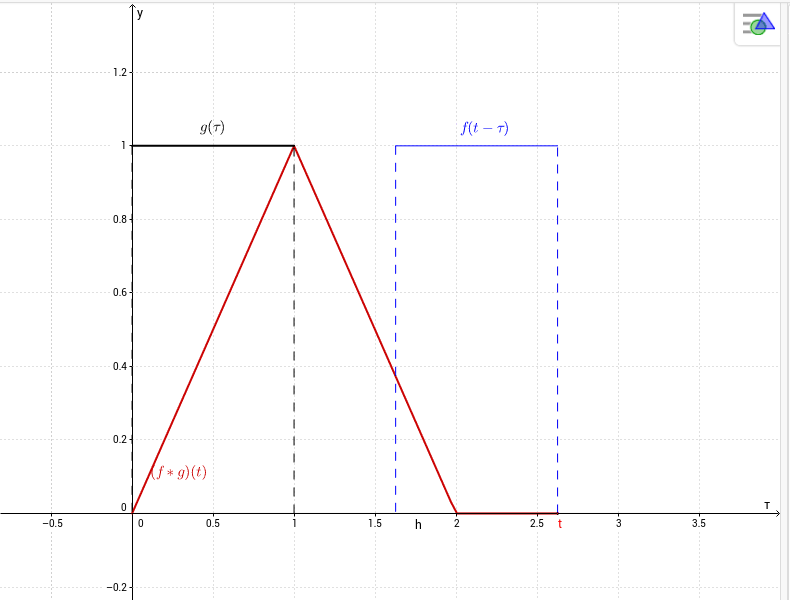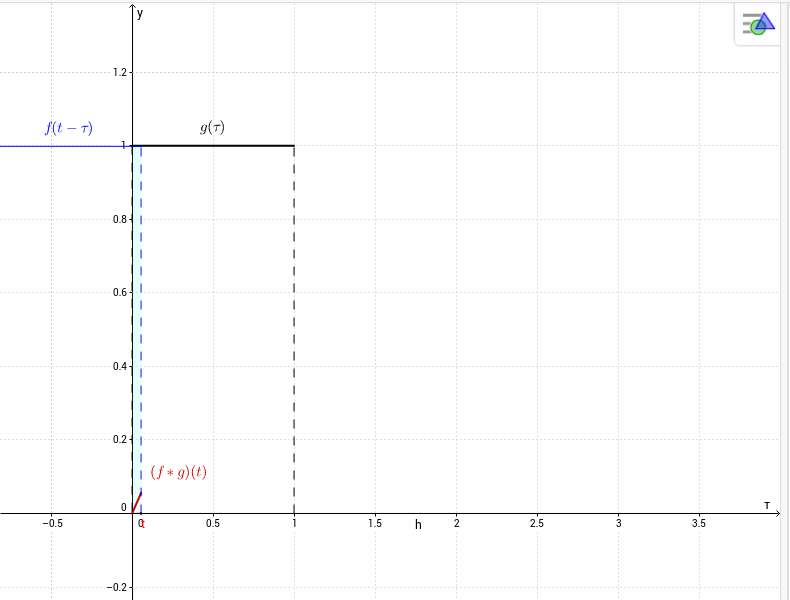
$$(f*g)(t)=\int_0^tf(t-\tau)g(\tau)d\tau =\begin{cases}
\int_0^td\tau=t,&\mbox{ se } 0< t< 1,\\
\int_{t-1}^1d\tau=2-t,&\mbox{ se } 1\le t<2,\\
0,&\mbox{ se } t\ge 2.
\end{cases} $$
- A convolução de duas funções $f:\mathbb{R}\to\mathbb{R}$ e
$g:\mathbb{R}\to\mathbb{R}$ seccionalmente contínuas, limitadas e tais que
$\int_{-\infty}^\infty |f(x)|dx<\infty$ e $\int_{-\infty}^\infty
|g(x)|dx<\infty$, é
definida por
$$
(f*g)(x)=\int_{-\infty}^\infty
f(y)g(x-y)dy,\quad\mbox{para }x\in\mathbb{R}.
$$
Seja $f:\mathbb{R}\to\mathbb{R}$ definida por $f(x)=\chi_{[0,1]}(x)=\begin{cases}1,\;\mbox{se }0\le x\le 1,\\0,\;\mbox{caso contrário.}\end{cases}$
\begin{eqnarray*}
(f*f)(x) &=& \int_{-\infty}^\infty
\chi_{[0,1]}(y)\chi_{[0,1]}(x-y)dy=\int_0^1
\chi_{[0,1]}(x-y)dy\\&=&\int_0^1
\chi_{[-1,0]}(y-x)dy=\int_0^1
\chi_{[-1+x,x]}(y)dy
= \left\{\begin{array}{cl}
0, & \mbox{se }x< 0, \\
x, & \mbox{se }0\le x< 1, \\
2-x, & \mbox{se }1\le x< 2, \\
0, & \mbox{se }x\ge 2.
\end{array}
\right.
\end{eqnarray*}
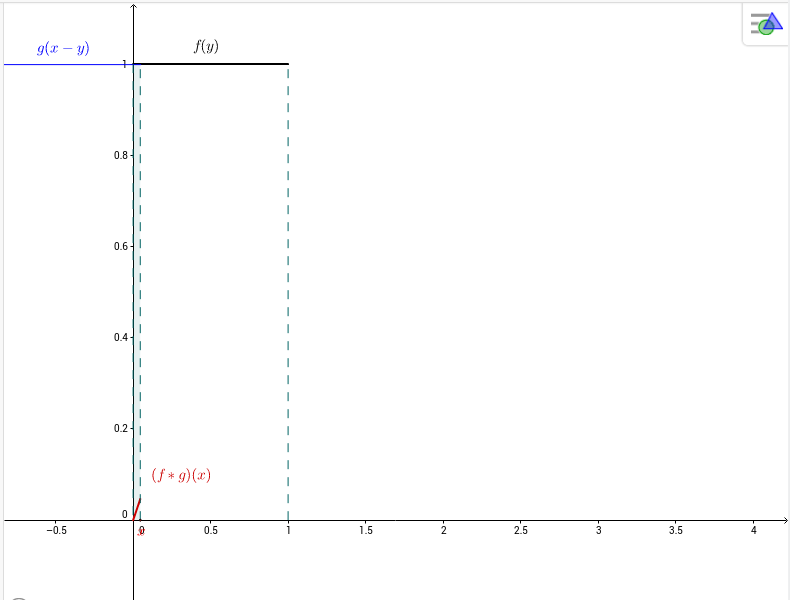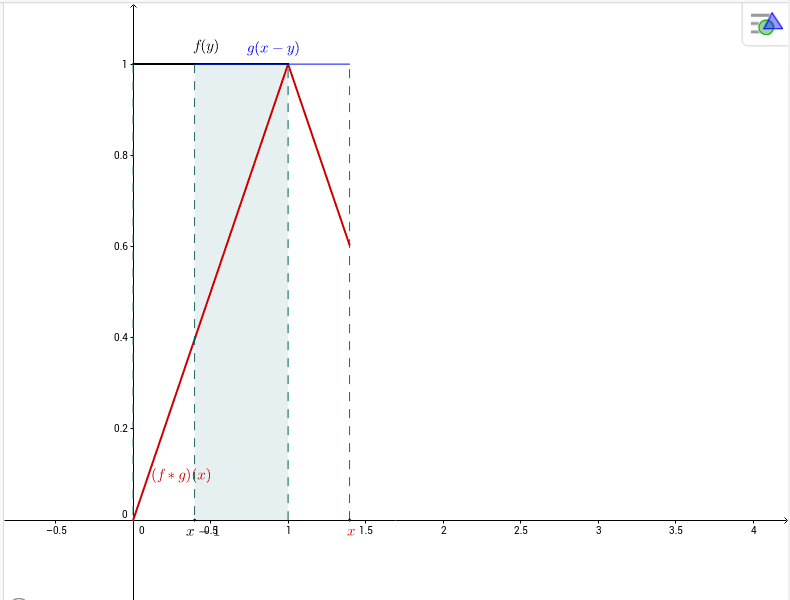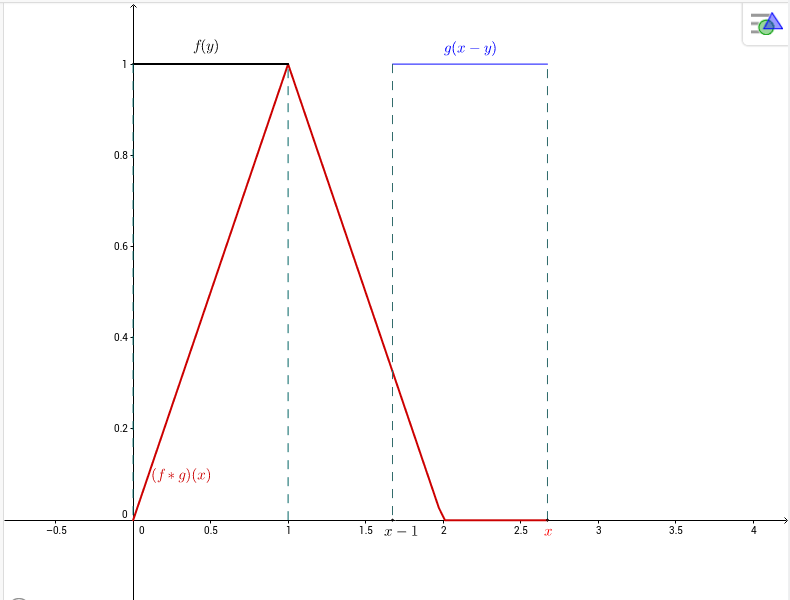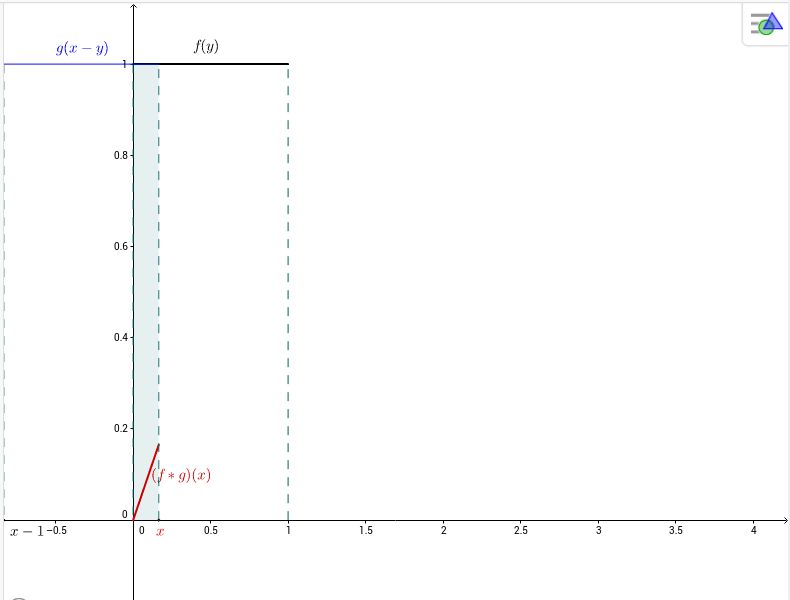
Página Inicial