Geometricamente, vetores são representados por segmentos (de retas) orientados (segmentos de retas com um sentido de percurso) no plano ou no espaço. A ponta da seta do segmento orientado é chamada ponto final ou extremidade e o outro ponto extremo é chamado de ponto inicial ou origem do segmento orientado.

Segmentos orientados com mesma direção, mesmo sentido e mesmo comprimento representam o mesmo vetor. A direção, o sentido e o comprimento do vetor são definidos como sendo a direção, o sentido e o comprimento de qualquer um dos segmentos orientados que o representam.

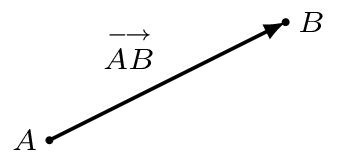
Se o ponto inicial de um representante de um vetor $V$ é $A$ e o ponto final é $B$, então escrevemos $$V=\stackrel{\longrightarrow}{AB}$$

---

A soma, $V+W$, de dois vetores $V$ e $W$ é definida pelo vetor obtido da seguinte forma:

1. tome um segmento orientado que representa $V$;
2. tome um segmento orientado que representa $W$, com origem na extremidade de $V$;
3. o vetor $V+W$ é representado pelo segmento orientado que vai da origem de $V$ até a extremidade de $W$.

Observamos também que a soma $V+W$ está na diagonal do paralelogramo determinado por $V$ e $W$, quando estão representados com a mesma origem.

---

A multiplicação de um vetor $V$ por um escalar $\alpha$, $\alpha\,V$, se $\alpha\ne 0$ e $V\ne\bar{0}$, é definida pelo vetor caracterizado por:

1. tem comprimento $|\alpha|$ vezes o comprimento de $V$,
2. a direção é a mesma de $V$ (neste caso, dizemos que eles são paralelos),
3. tem o mesmo sentido de $V$, se $\alpha\gt 0$ e tem o sentido contrário ao de $V$, se $\alpha\lt 0$.

Se $\alpha=0$ ou $V=\bar{0}$, definimos a multiplicação do vetor $V$ pelo escalar $\alpha$, como sendo o vetor nulo, $\alpha\,V=\bar{0}$.

Se $W=\alpha\,V$, dizemos que $W$ é um múltiplo escalar de $V$. Observe que dois vetores não nulos são paralelos (ou colineares) se, e somente se, um é um múltiplo escalar do outro.

---

Seja $V$ um vetor no plano. Definimos as componentes de $V$ como sendo as coordenadas $(v_1,v_2)$ do ponto final do representante de $V$ que tem ponto inicial na origem. Vamos identificar o vetor com as suas componentes e vamos escrever simplesmente

$V=(v_1,v_2)$.

Assim, as coordenadas de um ponto $P$ são iguais as componentes do vetor $\stackrel{\longrightarrow}{OP}$, que vai da origem do sistema de coordenadas ao ponto $P$. Em particular, o vetor nulo, $\bar{0}=(0,0)$.

• A soma de dois vetores no plano $V=(v_1,v_2)$ e $W~=~(w_1,w_2)$ é dada por
  $V+W=(v_1+w_1,v_2+w_2);$

• A multiplicação de um vetor no plano $V=(v_1,v_2)$ por um escalar $\alpha$ é dada por
  $\alpha\;V=(\alpha\, v_1,\alpha\, v_2).$

---

Seja $V$ um vetor no espaço. Definimos as componentes de $V$ como sendo as coordenadas $(v_1,v_2,v_3)$ do ponto final do representante de $V$ que tem ponto inicial na origem. Também identificamos o vetor com as suas componentes e vamos escrever

$V=(v_1,v_2,v_3)$.

Para vetores no espaço a soma de vetores e a multiplicação de vetor por escalar podem ser realizadas em termos das componentes.

• Se $V=(v_1,v_2,v_3)$ e $W=(w_1,w_2,w_3)$, então a adição de $V$ com $W$ é dada por
  $V+W=(v_1+w_1,v_2+w_2,v_3+w_3);$

• Se $V=(v_1,v_2,v_3)$ e $\alpha$ é um escalar, então a multiplicação de $V$ por $\alpha$ é dada por
  $\alpha\;V=(\alpha\, v_1,\alpha\, v_2,\alpha\, v_3).$

---

Quando um vetor $V$ está representado por um segmento orientado com ponto inicial fora da origem, digamos em $P=(x_1,y_1,z_1)$, e ponto final em $Q~=~(x_2,y_2,z_2)$, então as componentes do vetor $V$ são dadas por

$V=\stackrel{\longrightarrow}{PQ}= \stackrel{\longrightarrow}{OQ}-\stackrel{\longrightarrow}{OP}= (x_2-x_1,y_2-y_1,z_2-z_1).$

Portanto, as componentes de $V$ são obtidas subtraindo-se as coordenadas do ponto $Q$ (extremidade) das do ponto $P$ (origem). O mesmo se aplica a vetores no plano.

---

Sejam $U, V$ e $W$ vetores e $\alpha$ e $\beta$ escalares. São válidas as seguintes propriedades:

1. $U+V=V+U$;
2. $(U+V)+W=U+(V+W)$;
3. $U+\bar{0}=U$;
4. $U+(-U)=\bar{0}$;
5. $\alpha(\beta U)=(\alpha\beta)U$;
6. $\alpha(U+V)=\alpha U+\alpha V$;
7. $(\alpha+\beta)U=\alpha U+\beta U$;
8. $1U=U$.

❮ 2.2 Determinantes 3.2 Produto Escalar e Projeção Ortogonal ❯