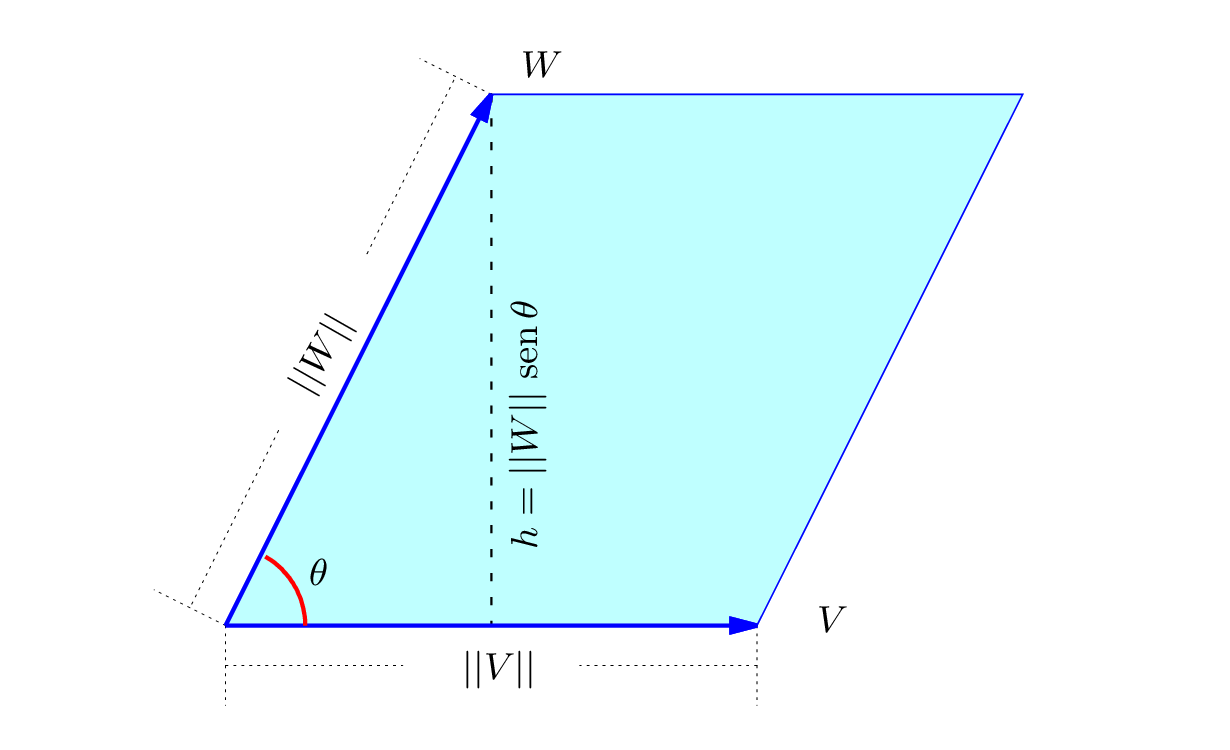
Sejam $V$ e $W$ dois vetores no espaço. Se os vetores forem não nulos, definimos o produto vetorial, $V \times W$, como sendo o vetor com as seguintes características:

1. Tem comprimento dado numericamente por $$||V\times W||=||V||\,||W||\,\sen\,\theta,$$ ou seja, a norma de $V\times W$ é numericamente igual à área do paralelogramo determinado por $V$ e $W$.
2. Tem direção perpendicular a $V$ e a $W$.
3. Tem o sentido dado pela regra da mão direita: Se o ângulo entre $V$ e $W$ é $\theta$, giramos o vetor $V$ de um ângulo $\theta$ até que coincida com $W$ e acompanhamos este movimento com os dedos da mão direita, então o polegar vai apontar no sentido de $V\times W$.

Se um dos vetores for o vetor nulo, o produto vetorial, $V \times W$, é definido como sendo o vetor nulo.

---

Sejam $U,V$ e $W$ vetores no espaço e $\alpha$ um escalar. São válidas as seguintes propriedades:

1. $V\times W = - (W\times V)$ (anti-comutatividade).
2. $V\times W=\bar{0}$ se, e somente se, $V=\alpha W$ ou $W=\alpha V$.
3. $(V\times W)\cdot V=(V\times W)\cdot W=0$.
4. $\alpha(V\times W)=(\alpha V)\times W=V\times (\alpha W)$.
5. $V\times (W+U)=V\times W+V\times U$ e $(V+W)\times U=V\times U+W\times U$ (Distributividade em relação a soma de vetores).

---

Os vetores canônicos

$\vec{i}=(1,0,0),\;$ $\;\vec{j}=(0,1,0)\;$ e $\;\vec{k}=(0,0,1)$

são vetores unitários (de norma igual à um) paralelos aos eixos coordenados.

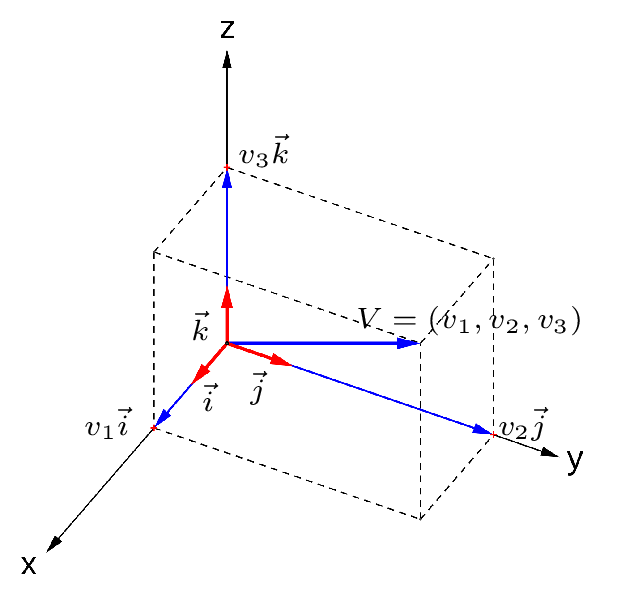
Todo vetor $$V=(v_1,v_2,v_3)$$ pode ser escrito como uma soma de múltiplos escalares de $\vec{i},\vec{j}$ e $\vec{k}$ (combinação linear), pois \begin{eqnarray} V=(v_1,v_2,v_3)&=&(v_1,0,0)+(0,v_2,0)+(0,0,v_3)=\nonumber \\&=&v_1(1,0,0)+v_2(0,1,0)+v_3(0,0,1)=\nonumber\\ &=& v_1\,\vec{i}+v_2\,\vec{j}+v_3\,\vec{k}.\label{vetcombijk} \end{eqnarray}

---

Sejam $V=(v_1,v_2,v_3)$ e $W=(w_1,w_2,w_3)$ vetores no espaço. Então o produto vetorial $V\times W$ é dado por \begin{equation}\label{edefpv} V\times W=\left( \det\left[\begin{array}{ll}v_2&v_3\\w_2&w_3 \end{array} \right], -\det\left[\begin{array}{ll}v_1&v_3\\w_1&w_3 \end{array} \right], \det\left[\begin{array}{ll}v_1&v_2\\w_1&w_2 \end{array} \right]\right). \end{equation}

Para obter as componentes do produto vetorial $V\times W$ procedemos como se segue:

1. Escreva a matriz: $$\left[\begin{array}{c}V\\W\end{array}\right]= \left[\begin{array}{lll}v_1&v_2&v_3\\ w_1&w_2&w_3\end{array}\right]\,;$$
2. Para calcular a primeira componente de $V\times W$, elimine a primeira coluna da matriz acima e calcule o determinante da sub-matriz resultante. A segunda componente é obtida, eliminando-se a segunda coluna e calculando-se o determinante da sub-matriz resultante com o sinal trocado. A terceira é obtida como a primeira, mas eliminando-se a terceira coluna.

Sejam $U=u_1\vec{i}+u_2\vec{j}+u_3\vec{k}$, $V=v_1\vec{i}+v_2\vec{j}+v_3\vec{k}$ e $W=w_1\vec{i}+w_2\vec{j}+w_3\vec{k}$. Então, $$(V\times W)\cdot U= \det\left[\begin{array}{lll} v_1&v_2&v_3\\ w_1&w_2&w_3\\ u_1&u_2&u_3 \end{array}\right]\,.$$

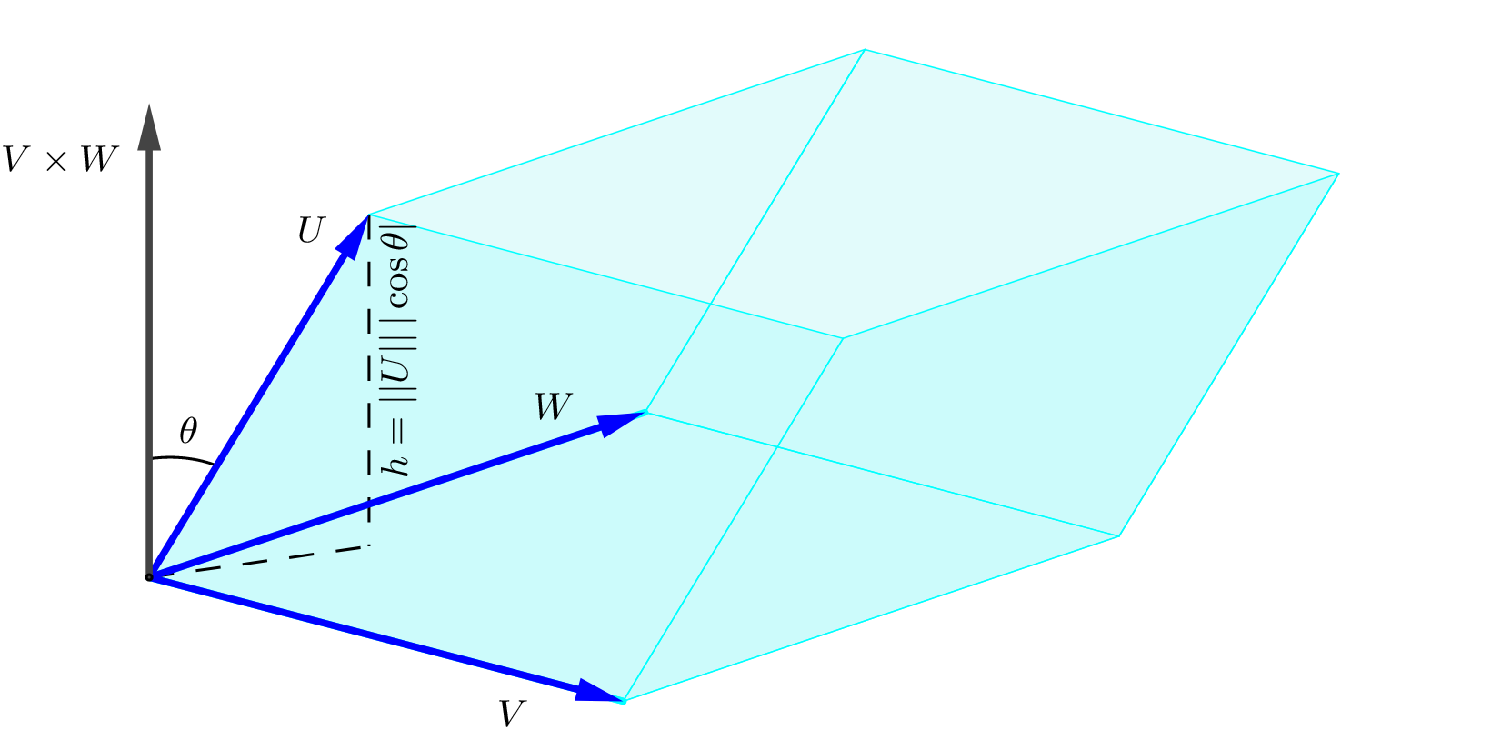
Dados três vetores no espaço, $U,V$ e $W$, $$ |(V\times W)\cdot U| $$ é numericamente igual ao volume do paralelepípedo determinado por $U,V$ e $W$.

---

Sejam $U=u_1\vec{i}+u_2\vec{j}+u_3\vec{k}$, $V=v_1\vec{i}+v_2\vec{j}+v_3\vec{k}$ e $W=w_1\vec{i}+w_2\vec{j}+w_3\vec{k}$. Estes vetores são coplanares (isto é, são paralelos a um mesmo plano) se, e somente se, $$(V\times W)\cdot U= \det\left[\begin{array}{lll} v_1&v_2&v_3\\ w_1&w_2&w_3\\ u_1&u_2&u_3 \end{array}\right]=0\,.$$

---

Sejam $U, V$ e $W$ vetores coplanares não nulos no espaço.

1. Então a equação vetorial $$xU+yV+zW=\bar{0}$$ tem solução não trivial, em que $x,y$ e $z$ são escalares.
2. Então um dos vetores $U, V$ ou $W$ é combinação linear (soma de múltiplos escalares) dos outros dois.
3. Se $V$ e $W$ são não paralelos, então $U$ é combinação linear de $V$ e $W$.

---

❮ 3.2 Produto Escalar e Projeção Ortogonal 4.1 Equações do Plano ❯