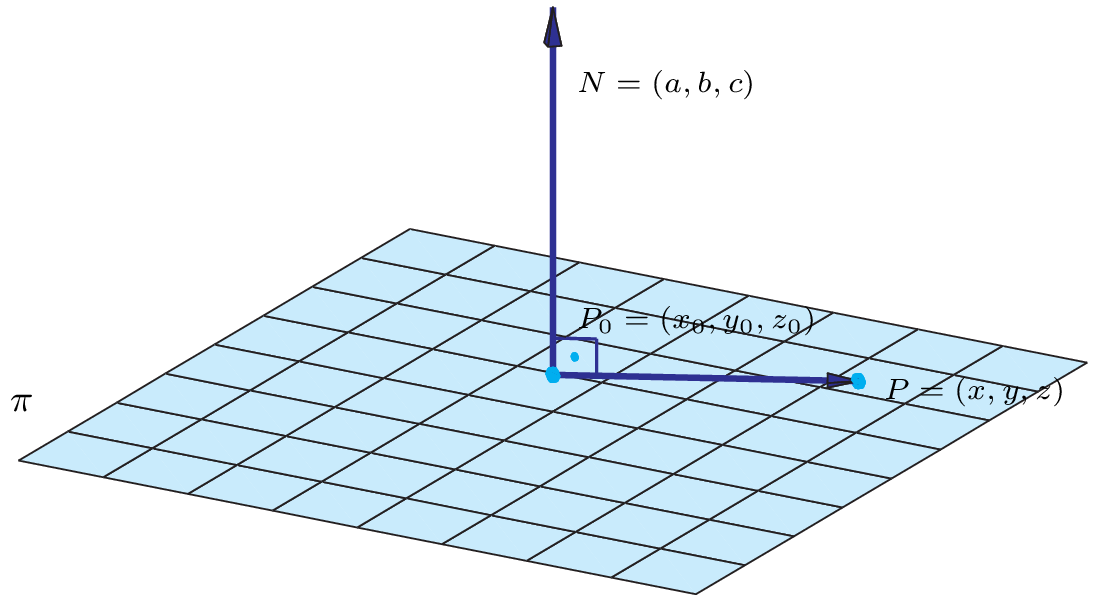
No espaço um plano é o conjunto dos pontos $P=(x,y,z)$ que satisfazem a equação $$ ax+by+cz+d=0,\quad \mbox{para }a,b,c,d\in\mathbb{R}, $$ que é chamada equação geral do plano.

---

A equação geral de um plano $\pi$ que passa por um ponto $P_0=(x_0,y_0,z_0)$ e tem vetor normal $N~=~(a,b,c)$ é \begin{equation}\label{egpl} ax+by+cz+d=0\,, \end{equation} em que $d=-(ax_0+by_0+cz_0)$ é obtido substiuindo-se o ponto $P_0=(x_0,y_0,z_0)$ na equação do plano.

---

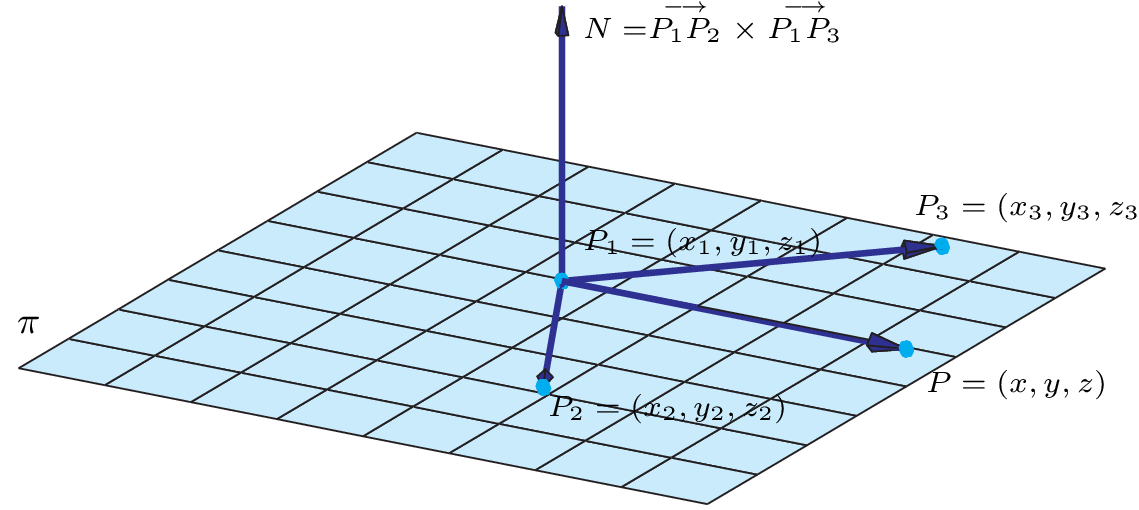
No espaço, a equação de um plano é determinada se são dados três pontos $P_1$, $P_2$ e $P_3$ não colineares (isto é, não pertencentes a uma mesma reta). Com os três pontos podemos ``formar'' os vetores $V=\stackrel{\longrightarrow}{P_1P_2}$ e $W=\stackrel{\longrightarrow}{P_1P_3}$.

O vetor $$N=V\times W= \stackrel{\longrightarrow}{P_1P_2}\times \stackrel{\longrightarrow}{P_1P_3}$$ é um vetor normal ao plano. Assim, a equação do plano é da forma $$ax+by+cz+d=0,$$ em que os coeficientes de $x,y$ e $z$ são as componentes do vetor $N$. Para determinar o coeficiente $d$, substituímos qualquer um dos pontos $P_1,P_2$ ou $P_3$ na equação do plano $\pi$.

Alternativamente, podemos encontrar a equação do plano da seguinte forma. Como vimos anteriormente, três vetores, $$\stackrel{\longrightarrow}{P_1P},\quad V=\stackrel{\longrightarrow}{P_1P_2}\quad \mbox{e}\quad W=\stackrel{\longrightarrow}{P_1P_3},$$ são coplanares se, e somente se, o produto misto entre eles é zero. Assim, um ponto $P~=~(x,y,z)$ pertence a $\pi$ se, e somente se, $$\stackrel{\longrightarrow}{P_1P}\cdot\,(\stackrel{\longrightarrow}{P_1P_2}\times \stackrel{\longrightarrow}{P_1P_3})=0\,,$$ ou seja, $$ \stackrel{\longrightarrow}{P_1P}\cdot\,(V\times W)= \det\left[\begin{array}{ccc} x-x_1&y-y_1&z-z_1\\ v_1&v_2&v_3\\ w_1&w_2&w_3 \end{array}\right]=0\,. $$

A equação do plano também é determinada se ao invés de serem dados três pontos, forem dados um ponto $P_1$ do plano e dois vetores paralelos ao plano, $V=(v_1,v_2,v_3)$ e $W=(w_1,w_2,w_3)$, desde que eles sejam não paralelos. Ou ainda se forem dados dois pontos $P_1$ e $P_2$ do plano e um vetor paralelo ao plano $V=(v_1,v_2,v_3)$ (não paralelo a $\stackrel{\longrightarrow}{P_1P_2}$), já que neste caso podemos formar o vetor $W~=~\stackrel{\longrightarrow}{P_1P_2}~=~(w_1,w_2,w_3)$ que é também paralelo ao plano.

Além da equação geral do plano podemos também caracterizar os pontos de um plano da seguinte forma. Considere um plano $\pi$, um ponto $P_0=(x_0,y_0,z_0)$ pertencente a $\pi$ e dois vetores $V=(v_1,v_2,v_3)$ e $W=(w_1,w_2,w_3)$ não colineares, paralelos a $\pi$. Um ponto $P=(x,y,z)$ pertence a $\pi$ se, e somente se, o vetor $\stackrel{\longrightarrow}{P_0P}=(x-x_0,y-y_0,z-z_0)$ é uma combinação linear de $V$ e $W$, ou seja, se existem escalares $t$ e $s$ tais que \begin{equation}\label{eqplavet} \stackrel{\longrightarrow}{P_0P}=tV+sW, \end{equation} ou ainda, $$(x-x_0,y-y_0,z-z_0)=(tv_1+sw_1,tv_2+sw_2,tv_3+sw_3).$$ Logo um ponto $P=(x,y,z)$ pertence a $\pi$ se, e somente se, satisfaz as equações $$\left\{ \begin{array}{rrrrrrr} x&=&x_0&+&v_1\,t&+&w_1\,s\\ y&=&y_0&+&v_2\,t&+&w_2\,s\\ z&=&z_0&+&v_3\,t&+&w_3\,s \end{array} \right. \quad\mbox{para $t,s\in\mathbb{R}$.} $$ Estas equações são chamadas equações paramétricas do plano.

❮ 3.3 Produtos Vetorial e Misto 4.2 Equações da Reta ❯