Um Curso de Geometria Analítica e Álgebra Linear: Resumos

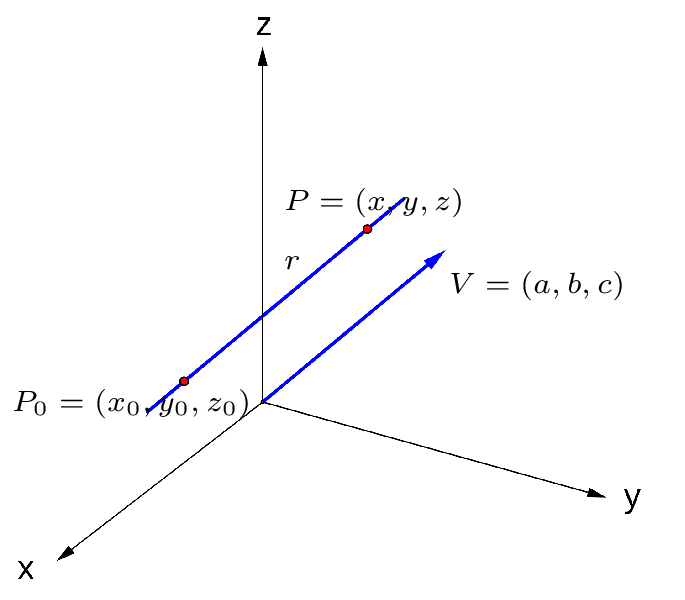
Vamos supor que uma reta $r$ seja paralela a um vetor $V=(a,b,c)$ não nulo e que passe por um ponto $P_0=(x_0,y_0,z_0)$. Um ponto $P=(x,y,z)$ pertence a reta $r$ se, e somente se, o vetor $\stackrel{\longrightarrow}{P_0P}$ é paralelo ao vetor $V$, isto é, se o vetor $\stackrel{\longrightarrow}{P_0P}$ é um múltiplo escalar de $V$, ou seja, \begin{equation}\label{evre} \stackrel{\longrightarrow}{P_0P}=t\;V\,. \end{equation} Em termos de componentes, esta equação pode ser escrita como $$ (x-x_0,y-y_0,z-z_0)=(ta,tb,tc). $$ Logo, $x-x_0=t\,a$, $y-y_0=t\,b$ e $z-z_0=t\,c$. Ou seja, a reta $r$ pode ser descrita como sendo o conjunto dos pontos $P=(x,y,z)$ tais que \begin{equation}\label{epret} \left\{\begin{array}{lll} x&=&x_0+t\,a\\ y&=&y_0+t\,b,\\ z&=&z_0+t\,c\end{array}\right.\, \quad\mbox{para $t\in\mathbb{R}$.} \end{equation}

Estas equações são chamadas equações paramétricas da reta, $r$ que passa por um ponto $P_0=(x_0,y_0,z_0)$ e é paralela ao vetor $V=(a,b,c)$. Este vetor é chamado vetor diretor da reta $r$.

As equações paramétricas da reta podem ser interpretadas como as equações de movimento de uma partícula em movimento retilíneo uniforme com velocidade $V=(a,b,c)$ e que no instante $t=0$ estava no ponto $P_0=(x_0,y_0,z_0)$.

As equações paramétricas podem ser reescritas como $$(x,y,z)=(x_0+at,y_0+bt,z_0+ct),\quad\mbox{para $t\in\mathbb{R}$.}$$ que é chamada equação vetorial da reta $r$.

Se todas componentes do vetor diretor da reta $r$ são não nulos, podemos resolver cada uma das equações paramétricas para $t$ e igualar os resultados obtendo o que chamamos de equações na forma simétrica de $r$:

❮ 4.1 Equações do Plano 4.3 Ângulos e Distâncias ❯